Collatz: Różnice pomiędzy wersjami

Z Lem
Skocz do: nawigacji, wyszukiwania
(→‎Elementary Theory of Addition of Natural Numbers)
 
(Nie pokazano 142 pośrednich wersji utworzonych przez tego samego użytkownika)
Linia 1: Linia 1:
−
Nareszcie!<br />
+
Finally!<br />
−
Praca nad problemem trwała 83 lata.<br />
+
  
 +
Work on the problem took 83 years.<br />
 +
We succeeded. We are changing the status of the "Collatz conjecture" to [http://lem12.uksw.edu.pl/images/3/37/CollatzConjecturebecomesTheorem20Nov23.pdf]<br />
  
−
Udało się  zmienić statut z ''hipoteza Collatza'' na '''twierdzenie Collatza'''.<br />
 
−
Argumenty znajdziesz [http://lem12.uksw.edu.pl/images/a/a2/On-Collatz-thm-3-09-21.pdf tu].<br />
 
  
−
==Wprowadzenie==
 
−
Rozpatrzmy zdanie<br/>
 
−
dla każdej liczby naturalnej <math>n</math>, poniższy program ma obliczenie sończone<br/>
 
−
{| class="wikitable"
 
−
|-
 
−
'''while''' n<> 0 '''do'''<br/>
 
−
'''if''' nieparzyste(n) '''then''' n:=3n+1  '''else''' n:=n/2 '''fi'''<br/>
 
−
'''od''' <br/>
 
−
|}
 
  
−
Zaczynamy od uwagi, że prawdziwośc powyższego zdania pociaga za sobą prawdzowość tezy Collatza. Ale w  r.1937  nie istniały komputery ani języki programowania.
 
−
==Spostrzeżenie z r. 2004==
 
−
* algorytm nie potrzebuje operacji mnożenia,
 
−
* w strukturze algebraicznej, która jest niestandardowym modelem elementarnej teorii dodawania liczb naturalnychnasz algorytm ma obliczenie nieskończone.
 
−
* Tezy Collatza nie można udowodnić na podstawie aksjomatów elementarnej teorii dodawania liczb naturalnych.
 
−
==Poprawiamy sformułowanie tezy==
 
−
W standardowej strukturze liczb naturalnych z operacją dodawania
 
−
nasz program ma obliczenie skończone, dla każdego argumentu ''n''..
 
  
 +
June 5, 2022 version [https://dx.doi.org/10.2139/ssrn.4158238 '''Collatz theorem'''] submitted to TCS Journal.<br />
 +
A shortened and less formal version of the proof can be found here [http://lem12.uksw.edu.pl/images/9/9f/MainPointsProofCollatz.pdf].<br />
 +
==Introduction==
 +
Let's consider the statement<br/>
 +
for every natural number <math>n</math>, the following program <math>Cl</math> has a finite computation.<br/>
 +
<math>\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
 +
\quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
 +
\mathbf{od} \end{array}\right\} </math> <br />
 +
We begin by noting that the truth of the above statement entails the truth of Collatz's thesis as it was formulated before World War II. <br />
 +
But in 1937, neither computers nor programming languages existed.<br />
 +
On the other hand, the theory of algorithms did exist and was already well developed. The theory of recursive functions was developed in Göttingen (David Hilbert and his students), Budapest (Rozsza Pterer, Laszlo Kalmar), ...<br />
 +
In London, Alan Turing created the abstract Turing machine.<br />
 +
In Moscow, Kolmogorov and in Kazan, Maltsev explored the concept of a computable function.<br />
 
<br />
 
<br />
 +
In Warsaw, Alfred Tarski, together with his students Mojżesz Presburger and Stanisław Jaskowski, obtained important results concerning the theory of addition of natural numbers.
 +
 +
==Our observations from 2004==
 +
* The Collatz algorithm <math>Cl</math> does not require multiplication or division operations. Multiplying by 3 (because 3x=x+x+x) and dividing by 2 (a simple algorithm adding every other 1 is sufficient), is sufficient.
 +
* In the algebraic structure <math>\mathfrak{M}</math>, which is a non-standard model of the elementary theory of addition of natural numbers (there is one, see below), the algorithm <math>Cl</math> has an infinite computation for many arguments.
 +
* Therefore, the Collatz theorem cannot be proven based on the axioms of the elementary theory of addition of natural numbers.
 +
* Moreover, in the language of elementary theory of addition, there is no stopping formula for the Collatz algorithm! It is a corollary from the Goedel incompleteness theorem. <br />
 +
So what do we have to prove?
 +
 +
==Correct formulation of the Collatz theorem==
 +
In the standard structure of natural numbers with the addition operation,
 +
our program <math>Cl</math> has a finite computation for each argument ''n''.
 +
 +
==Stop formula==
 +
i.e.
 +
=== A necessary and sufficient condition for the computation to be finite===
 +
Therefore, we need to create a formula <math>\theta</math> (a logical expression) such that it evaluates to true if and only if the computation of the program <math>Cl</math> is finite. There are many such formulas in the language of program calculation, i.e. algorithmic logic.<br/>
 +
,<math>\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
 +
\quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
 +
\mathbf{od} \end{array}\right\} (n=1) </math>
 +
<br />
 +
The value of the <math>\theta</math> formula depends only on the initial value of the "n" variable. This formula is satisfied by the value of the variable "n" if and only if the evaluation of the while ... program is finished and the final value of the variable "n" is equal to 1. <br />
 +
Other formulas can also be considered, e.g., <br />
 +
,<math>\qquad \xi:\,\bigcup \left\{\overbrace{\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\
 +
\quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
 +
\mathbf{fi} \end{array} }^{K}\right\} (n=1) </math> <br />
 +
{co reads: "there exists an iteration <math>K^i</math> of the program <math>K</math> such that after executing <math>K^i</math> the equality <math>n=1</math> is satisfied."} <br/>
 +
In other words, we are dealing with an upper bound on the values of the formulas <math>K^i(n=1)</math>, where <math>i= 0,1,2 \dots</math>.<br />
 +
 +
The second part of the problem is much more difficult: we must prove the stopping formula using the axioms of program calculus and the axioms of the algorithmic theory of natural numbers.<br/>
 +
 +
<br />
 +
==Elementary Theory of Addition of Natural Numbers==
 +
The previous observation that Collatz's theorem cannot be proved in this theory remains valid. However, the properties of the non-standard model of this theory and a few of its theorems will be helpful in further considerations.<br />
 +
<br />
 +
This theory is defined by specifying three components:
 +
*  the language,
 +
* the logic, i.e., the consequence operation, and
 +
* the axioms specific to this theory.<br />
 +
'''Language.''' The expressions of the language are composed of the following symbols: variable symbols, e.g., x, y, n, the + symbol for a binary operation, the = symbol for a binary relation, constant symbols, logical functor symbols, and auxiliary symbols, e.g., parentheses.<br />
 +
. Examples of expressions are...<br />
 +
 +
'''Logic.''' The consequence (inference) operation is determined by specifying the axioms of first-order logic and the rules of inference.<br />
 +
'''Axioms.'''
 +
<math>
 +
\begin{align}
 +
\tag{a}  \forall_x\ x+1 &\neq 0  \\
 +
\tag{b}  \forall_x\, \forall_y\ x+1=y+1 &\implies  x=y  \\
 +
\tag{c}  \forall_{x}\ x+0&=x  \\
 +
\tag{d}  \forall_{x,y}\ (y+1)+x&=(y+x)+1  \\
 +
\tag{I}    \Phi(0)\land \forall_x\,[\Phi(x) \implies \Phi(x+1)]&\implies \forall_x\Phi(x) 
 +
\end{align}   
 +
  </math>
 +
The expression <math>\Phi(x)</math> may be replaced by any formula.  The result is an axiom of theory
 +
This is the induction scheme.  <br />
 +
  We augment the set of axioms adding four axioms that define a coiple of useful notions. <br />
 +
  <math>
 +
\begin{align}
 +
  \tag{e}  even(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y  \\
 +
% \tag{o}  odd(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y+1  \\
 +
% \tag{D2}  x\, div\, 2 = y &\equiv (x=y+y\, \lor\, x=y+y+1)  \\
 +
% \tag{3x}  3x&\stackrel{df}{=} x+x+x
 +
\end{align}
 +
</math>
 +
 +
'''Models of Presburger Arithmetic'''<br />
 +
As expected, the sequence of standard values 0, 1, 2, 3, ... is a model of this theory.
 +
 +
Stanisław Jaśkowski discovered another, nonstandard model of Presburger arithmetic in 1929.
 +
 +
[[File:MonStandardModel.png|center|thumb|600px|Nonstandard model of Presburger arithmetic]]
 +
The universe of the model is a subset of the set of complex numbers <math>a+\math b</math>
 +
where <math>a \in \mathbb{Z} </math> i.e. a is an integer number and <math>b \in \mathbb{Q}^+ </math> is a positive rational number. Additionally, whenever <math>b=0 </math> we have <math>a>0</math>.
 +
Addition is defined as usual addition of complex numbers.
 +
 +
Both models are computable. There are also unpredictable models with arbitrarily high power.
 +
 +
==Algorithmic Theory of Natural Numbers==
 +
* Language. The alphabet of a language contains a set of variables, e.g., x,y. a functor + a two-argument addition operation, two constants 0 and 1, a relation sign = equality.<br />
 +
Terms (i.e., nomenclature expressions): this is the smallest set of expressions containing variables, constants, and closed under the combination of two terms in this way (t1 + t2).<br />
 +
Formulae.
 +
* Logic. Program calculus. Program calculus includes first-order logic. In addition to first-order formulas, the language of program calculus also contains algorithmic formulas. The simplest such formula is a string consisting of a program and a formula (usually a first-order formula) following it.
 +
To the axioms of first-order logic, axioms describing the properties of program-generating connectives should be added; see [[Algorithmic Logic]].
 +
To the inference rules of first-order logic, rules specific to program calculus should be added.<br />
 +
 +
* Axioms of the theory.<br />
 +
Only three formulas.<br />
 +
<math>
 +
\begin{eqnarray}
 +
\tag{ATN1} \forall_x\, x+1 \neq 0 &&\\
 +
\tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\
 +
\tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) &&
 +
\end{eqnarray} </math><br />
 +
 +
These are essentially the axioms of the successor theory.<br/>
 +
The ATN1 formula states that 0 is not the successor of any natural number.<br/>
 +
The ATN2 formula states that the successor is a one-to-one function.<br/>
 +
The formula ATN3 states that every natural number is ''reachable'' from zero by adding a finite number of ones.<br/>
 +
In this theory, one can write definitions for addition, multiplication, and any computable function.
 +
 +
==Analiza formuły stopu==
 +
xxx
 +
 +
==Trójki ==
 +
Spostrzeżenie (wynikłe z przygladania się formule stopu).<br />
 +
 +
<math>\forall_{n \neq 0} \exists_{x,y,z}\ n \cdot 3^x+y=2^z  </math>
 +
 +
==Drzewo Collatza==
 +
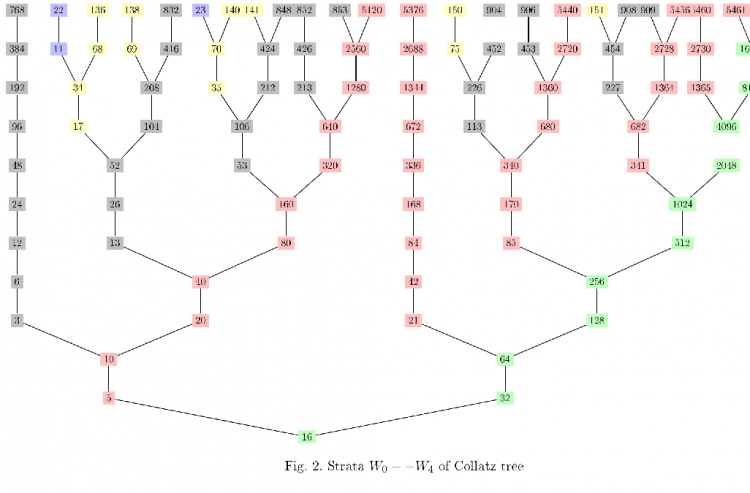
[[Plik:StratDrzewoCollatza.png|thumb|center |750px| Rys. 1  Fragmenty warstw <math>W_0, \dots W_4  </math> drzewa Collatza ]]
 +
 +
==Własności obliczeń na trójkach==
 +
Tutaj napiszemy więcej<br />
 +
==Kalejdoskop==
 +
 +
Oglądaj rysunki, wykonuj obliczenia, rozwiązuj zadania, formułuj swoje zdanie, próbuj je uzasadnić, ...<br />
 +
 +
Tu znajdziesz ....<br />
 +
===Obliczenia utemperowane===
 +
[[Plik:ObliczN19.pdf.png|thumb|center|750px|Utemperowane obliczenie dla n=76]]
 +
Trzy zadania. Odpowiedz czy są one jakos powiązane?<br />
 +
* Masz do dyspozycji bardzo wiele trójkątnych płytek, w dwu kolorach.
 +
Czy potrafisz ułożyć chodnik łączący posesje o numerze n z numerem 1?
 +
*[[Ułamek piętrowy]]
 +
* Czy obliczenie 3x+1 jest skończone dla każdej liczby naturalnej?
 +
 +
===Struktury algebraiczne===
 +
Struktura liczb naturalnych. <br />
 +
Algebra Jaśkowskiego.<br />
 +
===Teorie===
 +
elementarna teoria liczb naturalnych z dodawaniem.<br />
 +
algorytmiczna teoria  liczb naturalnych<br />
 +
===Zadania===
 +
 +
 +
<math>\alpha</math><br />
 +
 +
== Archiwum kolejnych wersji pracy ==
 +
[CollatzConjecturebecomesTheorem11Aug23    http://lem12.uksw.edu.pl/images/3/3b/CollatzConjecturebecomesTheorem11Aug23.pdf]
 +
 +
[https://dx.doi.org/10.2139/ssrn.4158238 \On Collatz theorem II.pdf wersja z 5 czerwca 2022 ]
 +
 +
][http://lem12.uksw.edu.pl/images/a/ab/On-Collatz-thm17-09-21.pdf wersja z 20 wrzesnia 2021]
 +
 +
[http://lem12.uksw.edu.pl/images/7/7d/Algorytmy-bliskie-Collatzowi.pdf  algorytmy wokół Collatzowe]
 +
 +
[http://lem12.uksw.edu.pl/images/c/c0/On-Collatz-thm-27-09-21.pdf  wersja z 27 wrzesnia 2021]
 +
 +
[http://lem12.uksw.edu.pl/images/8/8f/On-Collatz-thm-7-10-21.pdf  wersja z 7 pażdziernika 2021]

Aktualna wersja na dzień 10:17, 13 sie 2025

Finally!

Work on the problem took 83 years.
We succeeded. We are changing the status of the "Collatz conjecture" to [1]



June 5, 2022 version Collatz theorem submitted to TCS Journal.
A shortened and less formal version of the proof can be found here [2].

Introduction

Let's consider the statement
for every natural number [math]n[/math], the following program [math]Cl[/math] has a finite computation.
[math]\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ \quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ \mathbf{od} \end{array}\right\} [/math]
We begin by noting that the truth of the above statement entails the truth of Collatz's thesis as it was formulated before World War II.
But in 1937, neither computers nor programming languages existed.
On the other hand, the theory of algorithms did exist and was already well developed. The theory of recursive functions was developed in Göttingen (David Hilbert and his students), Budapest (Rozsza Pterer, Laszlo Kalmar), ...
In London, Alan Turing created the abstract Turing machine.
In Moscow, Kolmogorov and in Kazan, Maltsev explored the concept of a computable function.

In Warsaw, Alfred Tarski, together with his students Mojżesz Presburger and Stanisław Jaskowski, obtained important results concerning the theory of addition of natural numbers.

Our observations from 2004

  • The Collatz algorithm [math]Cl[/math] does not require multiplication or division operations. Multiplying by 3 (because 3x=x+x+x) and dividing by 2 (a simple algorithm adding every other 1 is sufficient), is sufficient.
  • In the algebraic structure [math]\mathfrak{M}[/math], which is a non-standard model of the elementary theory of addition of natural numbers (there is one, see below), the algorithm [math]Cl[/math] has an infinite computation for many arguments.
  • Therefore, the Collatz theorem cannot be proven based on the axioms of the elementary theory of addition of natural numbers.
  • Moreover, in the language of elementary theory of addition, there is no stopping formula for the Collatz algorithm! It is a corollary from the Goedel incompleteness theorem.

So what do we have to prove?

Correct formulation of the Collatz theorem

In the standard structure of natural numbers with the addition operation, our program [math]Cl[/math] has a finite computation for each argument n.

Stop formula

i.e.

A necessary and sufficient condition for the computation to be finite

Therefore, we need to create a formula [math]\theta[/math] (a logical expression) such that it evaluates to true if and only if the computation of the program [math]Cl[/math] is finite. There are many such formulas in the language of program calculation, i.e. algorithmic logic.
,[math]\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ \quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ \mathbf{od} \end{array}\right\} (n=1) [/math]
The value of the [math]\theta[/math] formula depends only on the initial value of the "n" variable. This formula is satisfied by the value of the variable "n" if and only if the evaluation of the while ... program is finished and the final value of the variable "n" is equal to 1.
Other formulas can also be considered, e.g.,
,[math]\qquad \xi:\,\bigcup \left\{\overbrace{\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\ \quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ \mathbf{fi} \end{array} }^{K}\right\} (n=1) [/math]
{co reads: "there exists an iteration [math]K^i[/math] of the program [math]K[/math] such that after executing [math]K^i[/math] the equality [math]n=1[/math] is satisfied."}
In other words, we are dealing with an upper bound on the values of the formulas [math]K^i(n=1)[/math], where [math]i= 0,1,2 \dots[/math].

The second part of the problem is much more difficult: we must prove the stopping formula using the axioms of program calculus and the axioms of the algorithmic theory of natural numbers.


Elementary Theory of Addition of Natural Numbers

The previous observation that Collatz's theorem cannot be proved in this theory remains valid. However, the properties of the non-standard model of this theory and a few of its theorems will be helpful in further considerations.

This theory is defined by specifying three components:

  • the language,
  • the logic, i.e., the consequence operation, and
  • the axioms specific to this theory.

Language. The expressions of the language are composed of the following symbols: variable symbols, e.g., x, y, n, the + symbol for a binary operation, the = symbol for a binary relation, constant symbols, logical functor symbols, and auxiliary symbols, e.g., parentheses.
. Examples of expressions are...

Logic. The consequence (inference) operation is determined by specifying the axioms of first-order logic and the rules of inference.
Axioms. [math] \begin{align} \tag{a} \forall_x\ x+1 &\neq 0 \\ \tag{b} \forall_x\, \forall_y\ x+1=y+1 &\implies x=y \\ \tag{c} \forall_{x}\ x+0&=x \\ \tag{d} \forall_{x,y}\ (y+1)+x&=(y+x)+1 \\ \tag{I} \Phi(0)\land \forall_x\,[\Phi(x) \implies \Phi(x+1)]&\implies \forall_x\Phi(x) \end{align} [/math] The expression [math]\Phi(x)[/math] may be replaced by any formula. The result is an axiom of theory This is the induction scheme. 

 	We augment the set of axioms adding four axioms that define a coiple of useful notions. 

  [math]
	\begin{align}
	  	\tag{e}  even(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y  \\
	%	\tag{o}  odd(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y+1  \\
	%	\tag{D2}  x\, div\, 2 = y &\equiv (x=y+y\, \lor\, x=y+y+1)  \\
	%	\tag{3x}  3x&\stackrel{df}{=} x+x+x
	\end{align} 
[/math]

Models of Presburger Arithmetic
As expected, the sequence of standard values 0, 1, 2, 3, ... is a model of this theory.

Stanisław Jaśkowski discovered another, nonstandard model of Presburger arithmetic in 1929.

Nonstandard model of Presburger arithmetic

The universe of the model is a subset of the set of complex numbers [math]a+\math b[/math] where [math]a \in \mathbb{Z} [/math] i.e. a is an integer number and [math]b \in \mathbb{Q}^+ [/math] is a positive rational number. Additionally, whenever [math]b=0 [/math] we have [math]a\gt0[/math]. Addition is defined as usual addition of complex numbers.

Both models are computable. There are also unpredictable models with arbitrarily high power.

Algorithmic Theory of Natural Numbers

  • Language. The alphabet of a language contains a set of variables, e.g., x,y. a functor + a two-argument addition operation, two constants 0 and 1, a relation sign = equality.

Terms (i.e., nomenclature expressions): this is the smallest set of expressions containing variables, constants, and closed under the combination of two terms in this way (t1 + t2).
Formulae.

  • Logic. Program calculus. Program calculus includes first-order logic. In addition to first-order formulas, the language of program calculus also contains algorithmic formulas. The simplest such formula is a string consisting of a program and a formula (usually a first-order formula) following it.

To the axioms of first-order logic, axioms describing the properties of program-generating connectives should be added; see Algorithmic Logic. To the inference rules of first-order logic, rules specific to program calculus should be added.

  • Axioms of the theory.

Only three formulas.
[math] \begin{eqnarray} \tag{ATN1} \forall_x\, x+1 \neq 0 &&\\ \tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\ \tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) && \end{eqnarray} [/math]

These are essentially the axioms of the successor theory.
The ATN1 formula states that 0 is not the successor of any natural number.
The ATN2 formula states that the successor is a one-to-one function.
The formula ATN3 states that every natural number is reachable from zero by adding a finite number of ones.
In this theory, one can write definitions for addition, multiplication, and any computable function.

Analiza formuły stopu

xxx

Trójki

Spostrzeżenie (wynikłe z przygladania się formule stopu).

[math]\forall_{n \neq 0} \exists_{x,y,z}\ n \cdot 3^x+y=2^z [/math]

Drzewo Collatza

Rys. 1 Fragmenty warstw [math]W_0, \dots W_4 [/math] drzewa Collatza

Własności obliczeń na trójkach

Tutaj napiszemy więcej

Kalejdoskop

Oglądaj rysunki, wykonuj obliczenia, rozwiązuj zadania, formułuj swoje zdanie, próbuj je uzasadnić, ...

Tu znajdziesz ....

Obliczenia utemperowane

Utemperowane obliczenie dla n=76

Trzy zadania. Odpowiedz czy są one jakos powiązane?

  • Masz do dyspozycji bardzo wiele trójkątnych płytek, w dwu kolorach.

Czy potrafisz ułożyć chodnik łączący posesje o numerze n z numerem 1?

  • Ułamek piętrowy
  • Czy obliczenie 3x+1 jest skończone dla każdej liczby naturalnej?

Struktury algebraiczne

Struktura liczb naturalnych.
Algebra Jaśkowskiego.

Teorie

elementarna teoria liczb naturalnych z dodawaniem.
algorytmiczna teoria liczb naturalnych

Zadania

[math]\alpha[/math]

Archiwum kolejnych wersji pracy

[CollatzConjecturebecomesTheorem11Aug23 http://lem12.uksw.edu.pl/images/3/3b/CollatzConjecturebecomesTheorem11Aug23.pdf]

\On Collatz theorem II.pdf wersja z 5 czerwca 2022

]wersja z 20 wrzesnia 2021

algorytmy wokół Collatzowe

wersja z 27 wrzesnia 2021

wersja z 7 pażdziernika 2021

Źródło „https://lem12.uksw.edu.pl/index.php?title=Collatz&oldid=3096”