Collatz: Różnice pomiędzy wersjami

Z Lem
Skocz do: nawigacji, wyszukiwania
(→‎Elementary Theory of Addition of Natural Numbers)
 
(Nie pokazano 71 pośrednich wersji utworzonych przez tego samego użytkownika)
Linia 1: Linia 1:
−
Nareszcie!<br />
+
Finally!<br />
−
Praca nad problemem trwała 83 lata.<br />
+
  
 +
Work on the problem took 83 years.<br />
 +
We succeeded. We are changing the status of the "Collatz conjecture" to [http://lem12.uksw.edu.pl/images/3/37/CollatzConjecturebecomesTheorem20Nov23.pdf]<br />
  
−
Udało się. Zmieniamy statut    ''hipotezy Collatza'' na
+
 
−
[https://dx.doi.org/10.2139/ssrn.4158238 '''twierdzenie Collatza'''].<br />
+
 
−
Argumenty znajdziesz http://lem12.uksw.edu.pl/wiki/Plik:MainPointsProofCollatz.pdf tutaj wersja z 5 czerwca 2022 ].<br />
+
 
−
Skróconą i niezbyt formalną wersję dowodu znajdziesz w tym [http://lem12.uksw.edu.pl/images/9/9f/MainPointsProofCollatz.pdf miejscu].<br />
+
June 5, 2022 version [https://dx.doi.org/10.2139/ssrn.4158238 '''Collatz theorem'''] submitted to TCS Journal.<br />
−
==Wprowadzenie==
+
A shortened and less formal version of the proof can be found here [http://lem12.uksw.edu.pl/images/9/9f/MainPointsProofCollatz.pdf].<br />
−
Rozpatrzmy zdanie<br/>
+
==Introduction==
−
dla każdej liczby naturalnej <math>n</math>, poniższy program <math>Cl </math> ma obliczenie sończone<br/>
+
Let's consider the statement<br/>
−
<math>\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
+
for every natural number <math>n</math>, the following program <math>Cl</math> has a finite computation.<br/>
−
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
+
<math>\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
 +
\quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
 
\mathbf{od} \end{array}\right\} </math> <br />
 
\mathbf{od} \end{array}\right\} </math> <br />
−
Zaczynamy od uwagi, że prawdziwośc powyższego zdania pociaga za sobą prawdzowość tezy Collatza, tak jak ona została sformułowana przed II wojną światową. <br />
+
We begin by noting that the truth of the above statement entails the truth of Collatz's thesis as it was formulated before World War II. <br />
−
Ale w  r.1937 nie istniały komputery ani języki programowania<br />
+
But in 1937, neither computers nor programming languages existed.<br />
−
.Z drugiej strony istniała i była już mocno rozwinięta teoria algorytmów. Teorię funkcji rekurencyjnych rozwijanow w Getyndze (David Hilbert i jego uczniowie), Budapeszcie (Rozsza Pterer, Laszlo Kalmar), ...<br />
+
On the other hand, the theory of algorithms did exist and was already well developed. The theory of recursive functions was developed in Göttingen (David Hilbert and his students), Budapest (Rozsza Pterer, Laszlo Kalmar), ...<br />
−
W Londynie Alan Turing stworzył abstrakcyjną maszynę Turinga.<br />
+
In London, Alan Turing created the abstract Turing machine.<br />
−
W Moskwie Kołmogorow i w Kazaniu Malcew badali pojęcie funkcji obliczalnej. <br />
+
In Moscow, Kolmogorov and in Kazan, Maltsev explored the concept of a computable function.<br />
 
<br />
 
<br />
−
W Warszawie Alfred Tarski wraz z uczniami Mojżeszem Presburgerem, Stanisławem Jaskowskim uzyskali ważne wyniki dotycące teorii dodawania liczb naturalnych.
+
In Warsaw, Alfred Tarski, together with his students Mojżesz Presburger and Stanisław Jaskowski, obtained important results concerning the theory of addition of natural numbers.
  
−
==Spostrzeżenie z r. 2004==
+
==Our observations from 2004==
−
* algorytm nie potrzebuje operacji mnożenia ani dzielenia przez 2,
+
* The Collatz algorithm <math>Cl</math> does not require multiplication or division operations. Multiplying by 3 (because 3x=x+x+x) and dividing by 2 (a simple algorithm adding every other 1 is sufficient), is sufficient.
−
* w strukturze algebraicznej, która jest niestandardowym modelem elementarnej teorii dodawania liczb naturalnych  (jest taka) algorytm <math>Cl</math> ma dla pewnych argumentów obliczenie nieskończone.
+
* In the algebraic structure <math>\mathfrak{M}</math>, which is a non-standard model of the elementary theory of addition of natural numbers (there is one, see below), the algorithm <math>Cl</math> has an infinite computation for many arguments.
−
* a więc tezy Collatza nie można udowodnić na podstawie aksjomatów elementarnej teorii dodawania liczb naturalnych,
+
* Therefore, the Collatz theorem cannot be proven based on the axioms of the elementary theory of addition of natural numbers.
−
* co więcej, w języku elementarnej teorii dodawania nie istnieje formuła stopu dl algorytmu Collatza!. Czego więc mamy dowieść?
+
* Moreover, in the language of elementary theory of addition, there is no stopping formula for the Collatz algorithm! It is a corollary from the Goedel incompleteness theorem. <br />
 +
So what do we have to prove?
  
−
==Poprawiamy sformułowanie tezy==
+
==Correct formulation of the Collatz theorem==
−
W standardowej strukturze liczb naturalnych z operacją dodawania
+
In the standard structure of natural numbers with the addition operation,
−
nasz program ma obliczenie skończone, dla każdego argumentu ''n''..
+
our program <math>Cl</math> has a finite computation for each argument ''n''.
−
==Formuła stopu==
+
 
−
Należy zatem stworzyć formułę <math>\theta</math> (wyrażenie logiczne) taką, że przyjmuje ona wrtośc prawda wtedy i tylko wtedy gdy obliczenie programu <math>Cl</math> jest skończone. Takich formuł jest wiele w języku urachunku programów, tj. logiki algorytmicznej.<br/>
+
==Stop formula==
−
,<math>\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
+
i.e.
−
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
+
=== A necessary and sufficient condition for the computation to be finite===
 +
Therefore, we need to create a formula <math>\theta</math> (a logical expression) such that it evaluates to true if and only if the computation of the program <math>Cl</math> is finite. There are many such formulas in the language of program calculation, i.e. algorithmic logic.<br/>
 +
,<math>\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
 +
\quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
 
\mathbf{od} \end{array}\right\} (n=1) </math>
 
\mathbf{od} \end{array}\right\} (n=1) </math>
 
<br />
 
<br />
−
Można też rozważać inne formuły, np, <br/>
+
The value of the <math>\theta</math> formula depends only on the initial value of the "n" variable. This formula is satisfied by the value of the variable "n" if and only if the evaluation of the while ... program is finished and the final value of the variable "n" is equal to 1. <br />
−
,<math>\qquad \xi:\,\bigcup \left\{K:\,\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\
+
Other formulas can also be considered, e.g., <br />
−
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
+
,<math>\qquad \xi:\,\bigcup \left\{\overbrace{\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\
−
\mathbf{fi} \end{array}\right\} (n=1) </math> <br/>
+
\quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
−
{co się czyta: ''istnieje taka iteracja ,<math>K^i</math> programu <math>K</math>, że po  wykonaniu  <math>K^i</math> zachodzi równość'' <math>n=1</math> .} <br/>
+
\mathbf{fi} \end{array} }^{K}\right\} (n=1) </math> <br />
−
Druga część zadania jest znacznie trudniejsza: nalezy przeprowadzić dowód formuły stopu posiłkując się aksjomatami rachunku programów i aksjomatami algorytmicznej teorii liczb naturalnych.<br/>
+
{co reads: "there exists an iteration <math>K^i</math> of the program <math>K</math> such that after executing <math>K^i</math> the equality <math>n=1</math> is satisfied."} <br/>
 +
In other words, we are dealing with an upper bound on the values of the formulas <math>K^i(n=1)</math>, where <math>i= 0,1,2 \dots</math>.<br />
 +
 
 +
The second part of the problem is much more difficult: we must prove the stopping formula using the axioms of program calculus and the axioms of the algorithmic theory of natural numbers.<br/>
  
 
<br />
 
<br />
−
==Elementarna teoria dodawania liczb naturalnych==
+
==Elementary Theory of Addition of Natural Numbers==
−
Poprzednia obserwacja stwierdzająca, że w tej teorii nie można przeprowadzić dowodu tezy Collatza pozostaje w mocy. Jednak, w dalszych rozważaniach pomocne będą własności niestandardowego modelu tej teorii a także parę twierdzeń tej teorii.<br />
+
The previous observation that Collatz's theorem cannot be proved in this theory remains valid. However, the properties of the non-standard model of this theory and a few of its theorems will be helpful in further considerations.<br />
 
<br />
 
<br />
−
Teoria ta jest wyznaczona przez podanie trzech składników: języka, logiki czyli operacji konsekencji oraz aksjomatów specyficznych dla tej teorii. <br />
+
This theory is defined by specifying three components:
−
'''Język.''' Wyrażenia języka zbudowane są z następujących symboli: symbole zmiennych np. x,y,n, symbou  + dwuargumentoweji operacji, symbolu = dwuargumentowej relacji, symboli 0,1 stałych i symboli funktorów logicznych oraz symboli pomocniczych np. nawiasy<br />
+
*  the language,
−
.
+
* the logic, i.e., the consequence operation, and
−
Przykładami wyrażeń są ...<br />
+
* the axioms specific to this theory.<br />
 +
'''Language.''' The expressions of the language are composed of the following symbols: variable symbols, e.g., x, y, n, the + symbol for a binary operation, the = symbol for a binary relation, constant symbols, logical functor symbols, and auxiliary symbols, e.g., parentheses.<br />
 +
. Examples of expressions are...<br />
  
−
'''Logika.''' Operacja konsekwencji (wnioskowania) jest wyznaczona przez podanie aksjomatów logiki pierwszego rzędu i reguł wnioskowania. <br />
+
'''Logic.''' The consequence (inference) operation is determined by specifying the axioms of first-order logic and the rules of inference.<br />
−
'''Aksjomaty.'''
+
'''Axioms.'''
 +
<math>
 +
\begin{align}
 +
\tag{a}  \forall_x\ x+1 &\neq 0  \\
 +
\tag{b}  \forall_x\, \forall_y\ x+1=y+1 &\implies  x=y  \\
 +
\tag{c}  \forall_{x}\ x+0&=x  \\
 +
\tag{d}  \forall_{x,y}\ (y+1)+x&=(y+x)+1  \\
 +
\tag{I}    \Phi(0)\land \forall_x\,[\Phi(x) \implies \Phi(x+1)]&\implies \forall_x\Phi(x) 
 +
\end{align}   
 +
  </math>
 +
The expression <math>\Phi(x)</math> may be replaced by any formula.  The result is an axiom of theory
 +
This is the induction scheme.  <br />
 +
  We augment the set of axioms adding four axioms that define a coiple of useful notions. <br />
 +
  <math>
 +
\begin{align}
 +
  \tag{e}  even(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y  \\
 +
% \tag{o}  odd(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y+1  \\
 +
% \tag{D2}  x\, div\, 2 = y &\equiv (x=y+y\, \lor\, x=y+y+1)  \\
 +
% \tag{3x}  3x&\stackrel{df}{=} x+x+x
 +
\end{align}
 +
</math>
  
−
==Algorytmiczna teoria liczb naturalnych==
+
'''Models of Presburger Arithmetic'''<br />
−
* Język.  Alfabet języka zawiera zbiór zmiennych, np. x,y. funktor + dwiargumentowego działania dodawania, dwie stałe 0 i 1, znak relacji = równości.<br />
+
As expected, the sequence of standard values 0, 1, 2, 3, ... is a model of this theory.
−
Termy (tj. wyrażenia nazwowe: jest to najmniejszy zbiór wyrażeeń zawierający zmienne, stałe i zamknięty ze wzgledu na lączenie dwu termów w ten sposób (t1 + t2).<br />
+
−
Formuły.  
+
−
* Logika. Rachunek programów. Rachunek programów zawiera w sobie logikę pierwszego rzędu. Język rachunku programów oprócz formuł pierwszego rzędu zaiera formuły algorytmiczne. Najprostsza taka formuła to napis składający się z programu i następującej po nim formuły (zwykle formuły pierwszego rzędu).
+
−
Do aksjomatów logiki pierszego rzędu należy dodać aksjomaty opisujące własności spójników programotwórczych, zob. [[Logika algorytmiczna]].
+
−
Do reguł wnioskowania logiki pierwszego rzędu należy dodać reguły specyficzne dla rachunku programów. <br />
+
  
−
* Aksjomaty teorii. <br />
+
Stanisław Jaśkowski discovered another, nonstandard model of Presburger arithmetic in 1929.
−
Tylko trzy formuły. <br />
+
 
−
<math>  
+
[[File:MonStandardModel.png|center|thumb|600px|Nonstandard model of Presburger arithmetic]]
 +
The universe of the model is a subset of the set of complex numbers <math>a+\math b</math>
 +
where <math>a \in \mathbb{Z} </math> i.e. a is an integer number and <math>b \in \mathbb{Q}^+ </math> is a positive rational number. Additionally, whenever <math>b=0 </math> we have <math>a>0</math>.
 +
Addition is defined as usual addition of complex numbers.
 +
 
 +
Both models are computable. There are also unpredictable models with arbitrarily high power.
 +
 
 +
==Algorithmic Theory of Natural Numbers==
 +
* Language. The alphabet of a language contains a set of variables, e.g., x,y. a functor + a two-argument addition operation, two constants 0 and 1, a relation sign = equality.<br />
 +
Terms (i.e., nomenclature expressions): this is the smallest set of expressions containing variables, constants, and closed under the combination of two terms in this way (t1 + t2).<br />
 +
Formulae.
 +
* Logic. Program calculus. Program calculus includes first-order logic. In addition to first-order formulas, the language of program calculus also contains algorithmic formulas. The simplest such formula is a string consisting of a program and a formula (usually a first-order formula) following it.
 +
To the axioms of first-order logic, axioms describing the properties of program-generating connectives should be added; see [[Algorithmic Logic]].
 +
To the inference rules of first-order logic, rules specific to program calculus should be added.<br />
 +
 
 +
* Axioms of the theory.<br />
 +
Only three formulas.<br />  
 +
<math>
 
\begin{eqnarray}
 
\begin{eqnarray}
−
\tag{ATN1} \forall_x\, x+1 \neq 0 &&\\
+
\tag{ATN1} \forall_x\, x+1 \neq 0 &&\\
−
\tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\
+
\tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\
−
\tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) &&
+
\tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) &&
−
\end{eqnarray}   </math><br />
+
\end{eqnarray} </math><br />
  
−
Są to właściwie aksjomaty teorii następnika.<br/>
+
These are essentially the axioms of the successor theory.<br/>
−
Formuła ATN1 stwierdza, że 0 nie jest następnikiem żadnej liczby naturalnej. <br/>
+
The ATN1 formula states that 0 is not the successor of any natural number.<br/>
−
Formuła ATN2 stwierdza, że następnik jest funkcją róznowartosciową. <br/>
+
The ATN2 formula states that the successor is a one-to-one function.<br/>
−
Formuła ATN3 stwierdza, że każda liczba naturalna jest ''osiągalna'' z zera przez dodanie skończonej liczby jedynek.<br/>
+
The formula ATN3 states that every natural number is ''reachable'' from zero by adding a finite number of ones.<br/>
−
W tej teorii można napisać definicje działań dodawania, mnożenia i każdej funkcji obliczalnej.
+
In this theory, one can write definitions for addition, multiplication, and any computable function.
  
 
==Analiza formuły stopu==
 
==Analiza formuły stopu==
Linia 87: Linia 130:
  
 
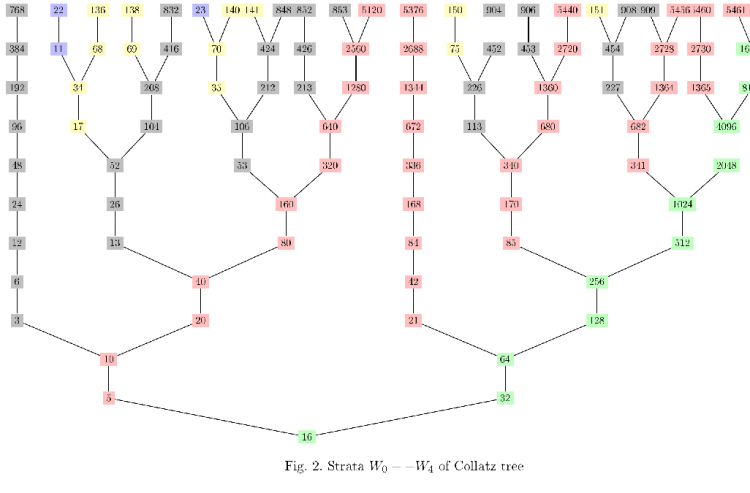
==Drzewo Collatza==
 
==Drzewo Collatza==
−
xxx
+
[[Plik:StratDrzewoCollatza.png|thumb|center |750px| Rys. 1  Fragmenty warstw <math>W_0, \dots W_4  </math> drzewa Collatza ]]
 +
 
 
==Własności obliczeń na trójkach==
 
==Własności obliczeń na trójkach==
 +
Tutaj napiszemy więcej<br />
 +
==Kalejdoskop==
 +
 +
Oglądaj rysunki, wykonuj obliczenia, rozwiązuj zadania, formułuj swoje zdanie, próbuj je uzasadnić, ...<br />
 +
 +
Tu znajdziesz ....<br />
 +
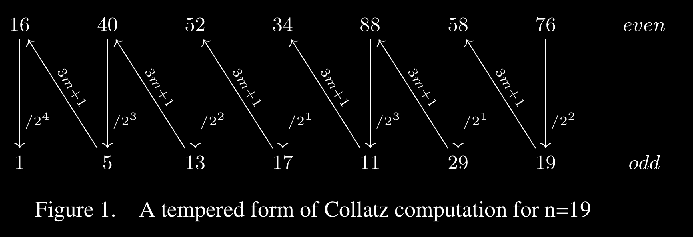
===Obliczenia utemperowane===
 +
[[Plik:ObliczN19.pdf.png|thumb|center|750px|Utemperowane obliczenie dla n=76]]
 +
Trzy zadania. Odpowiedz czy są one jakos powiązane?<br />
 +
* Masz do dyspozycji bardzo wiele trójkątnych płytek, w dwu kolorach.
 +
Czy potrafisz ułożyć chodnik łączący posesje o numerze n z numerem 1?
 +
*[[Ułamek piętrowy]]
 +
* Czy obliczenie 3x+1 jest skończone dla każdej liczby naturalnej?
 +
 +
===Struktury algebraiczne===
 +
Struktura liczb naturalnych. <br />
 +
Algebra Jaśkowskiego.<br />
 +
===Teorie===
 +
elementarna teoria liczb naturalnych z dodawaniem.<br />
 +
algorytmiczna teoria  liczb naturalnych<br />
 +
===Zadania===
 +
 +
 +
<math>\alpha</math><br />
  
 
== Archiwum kolejnych wersji pracy ==
 
== Archiwum kolejnych wersji pracy ==
 +
[CollatzConjecturebecomesTheorem11Aug23    http://lem12.uksw.edu.pl/images/3/3b/CollatzConjecturebecomesTheorem11Aug23.pdf]
 +
 
[https://dx.doi.org/10.2139/ssrn.4158238 \On Collatz theorem II.pdf wersja z 5 czerwca 2022 ]
 
[https://dx.doi.org/10.2139/ssrn.4158238 \On Collatz theorem II.pdf wersja z 5 czerwca 2022 ]
  

Aktualna wersja na dzień 10:17, 13 sie 2025

Finally!

Work on the problem took 83 years.
We succeeded. We are changing the status of the "Collatz conjecture" to [1]



June 5, 2022 version Collatz theorem submitted to TCS Journal.
A shortened and less formal version of the proof can be found here [2].

Introduction

Let's consider the statement
for every natural number [math]n[/math], the following program [math]Cl[/math] has a finite computation.
[math]\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ \quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ \mathbf{od} \end{array}\right\} [/math]
We begin by noting that the truth of the above statement entails the truth of Collatz's thesis as it was formulated before World War II.
But in 1937, neither computers nor programming languages existed.
On the other hand, the theory of algorithms did exist and was already well developed. The theory of recursive functions was developed in Göttingen (David Hilbert and his students), Budapest (Rozsza Pterer, Laszlo Kalmar), ...
In London, Alan Turing created the abstract Turing machine.
In Moscow, Kolmogorov and in Kazan, Maltsev explored the concept of a computable function.

In Warsaw, Alfred Tarski, together with his students Mojżesz Presburger and Stanisław Jaskowski, obtained important results concerning the theory of addition of natural numbers.

Our observations from 2004

  • The Collatz algorithm [math]Cl[/math] does not require multiplication or division operations. Multiplying by 3 (because 3x=x+x+x) and dividing by 2 (a simple algorithm adding every other 1 is sufficient), is sufficient.
  • In the algebraic structure [math]\mathfrak{M}[/math], which is a non-standard model of the elementary theory of addition of natural numbers (there is one, see below), the algorithm [math]Cl[/math] has an infinite computation for many arguments.
  • Therefore, the Collatz theorem cannot be proven based on the axioms of the elementary theory of addition of natural numbers.
  • Moreover, in the language of elementary theory of addition, there is no stopping formula for the Collatz algorithm! It is a corollary from the Goedel incompleteness theorem.

So what do we have to prove?

Correct formulation of the Collatz theorem

In the standard structure of natural numbers with the addition operation, our program [math]Cl[/math] has a finite computation for each argument n.

Stop formula

i.e.

A necessary and sufficient condition for the computation to be finite

Therefore, we need to create a formula [math]\theta[/math] (a logical expression) such that it evaluates to true if and only if the computation of the program [math]Cl[/math] is finite. There are many such formulas in the language of program calculation, i.e. algorithmic logic.
,[math]\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ \quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ \mathbf{od} \end{array}\right\} (n=1) [/math]
The value of the [math]\theta[/math] formula depends only on the initial value of the "n" variable. This formula is satisfied by the value of the variable "n" if and only if the evaluation of the while ... program is finished and the final value of the variable "n" is equal to 1.
Other formulas can also be considered, e.g.,
,[math]\qquad \xi:\,\bigcup \left\{\overbrace{\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\ \quad \mathbf{if}\ odd(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ \mathbf{fi} \end{array} }^{K}\right\} (n=1) [/math]
{co reads: "there exists an iteration [math]K^i[/math] of the program [math]K[/math] such that after executing [math]K^i[/math] the equality [math]n=1[/math] is satisfied."}
In other words, we are dealing with an upper bound on the values of the formulas [math]K^i(n=1)[/math], where [math]i= 0,1,2 \dots[/math].

The second part of the problem is much more difficult: we must prove the stopping formula using the axioms of program calculus and the axioms of the algorithmic theory of natural numbers.


Elementary Theory of Addition of Natural Numbers

The previous observation that Collatz's theorem cannot be proved in this theory remains valid. However, the properties of the non-standard model of this theory and a few of its theorems will be helpful in further considerations.

This theory is defined by specifying three components:

  • the language,
  • the logic, i.e., the consequence operation, and
  • the axioms specific to this theory.

Language. The expressions of the language are composed of the following symbols: variable symbols, e.g., x, y, n, the + symbol for a binary operation, the = symbol for a binary relation, constant symbols, logical functor symbols, and auxiliary symbols, e.g., parentheses.
. Examples of expressions are...

Logic. The consequence (inference) operation is determined by specifying the axioms of first-order logic and the rules of inference.
Axioms. [math] \begin{align} \tag{a} \forall_x\ x+1 &\neq 0 \\ \tag{b} \forall_x\, \forall_y\ x+1=y+1 &\implies x=y \\ \tag{c} \forall_{x}\ x+0&=x \\ \tag{d} \forall_{x,y}\ (y+1)+x&=(y+x)+1 \\ \tag{I} \Phi(0)\land \forall_x\,[\Phi(x) \implies \Phi(x+1)]&\implies \forall_x\Phi(x) \end{align} [/math] The expression [math]\Phi(x)[/math] may be replaced by any formula. The result is an axiom of theory This is the induction scheme. 

 	We augment the set of axioms adding four axioms that define a coiple of useful notions. 

  [math]
	\begin{align}
	  	\tag{e}  even(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y  \\
	%	\tag{o}  odd(x) &\stackrel{df}{\equiv} \exists_y\, x=y+y+1  \\
	%	\tag{D2}  x\, div\, 2 = y &\equiv (x=y+y\, \lor\, x=y+y+1)  \\
	%	\tag{3x}  3x&\stackrel{df}{=} x+x+x
	\end{align} 
[/math]

Models of Presburger Arithmetic
As expected, the sequence of standard values 0, 1, 2, 3, ... is a model of this theory.

Stanisław Jaśkowski discovered another, nonstandard model of Presburger arithmetic in 1929.

Nonstandard model of Presburger arithmetic

The universe of the model is a subset of the set of complex numbers [math]a+\math b[/math] where [math]a \in \mathbb{Z} [/math] i.e. a is an integer number and [math]b \in \mathbb{Q}^+ [/math] is a positive rational number. Additionally, whenever [math]b=0 [/math] we have [math]a\gt0[/math]. Addition is defined as usual addition of complex numbers.

Both models are computable. There are also unpredictable models with arbitrarily high power.

Algorithmic Theory of Natural Numbers

  • Language. The alphabet of a language contains a set of variables, e.g., x,y. a functor + a two-argument addition operation, two constants 0 and 1, a relation sign = equality.

Terms (i.e., nomenclature expressions): this is the smallest set of expressions containing variables, constants, and closed under the combination of two terms in this way (t1 + t2).
Formulae.

  • Logic. Program calculus. Program calculus includes first-order logic. In addition to first-order formulas, the language of program calculus also contains algorithmic formulas. The simplest such formula is a string consisting of a program and a formula (usually a first-order formula) following it.

To the axioms of first-order logic, axioms describing the properties of program-generating connectives should be added; see Algorithmic Logic. To the inference rules of first-order logic, rules specific to program calculus should be added.

  • Axioms of the theory.

Only three formulas.
[math] \begin{eqnarray} \tag{ATN1} \forall_x\, x+1 \neq 0 &&\\ \tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\ \tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) && \end{eqnarray} [/math]

These are essentially the axioms of the successor theory.
The ATN1 formula states that 0 is not the successor of any natural number.
The ATN2 formula states that the successor is a one-to-one function.
The formula ATN3 states that every natural number is reachable from zero by adding a finite number of ones.
In this theory, one can write definitions for addition, multiplication, and any computable function.

Analiza formuły stopu

xxx

Trójki

Spostrzeżenie (wynikłe z przygladania się formule stopu).

[math]\forall_{n \neq 0} \exists_{x,y,z}\ n \cdot 3^x+y=2^z [/math]

Drzewo Collatza

Rys. 1 Fragmenty warstw [math]W_0, \dots W_4 [/math] drzewa Collatza

Własności obliczeń na trójkach

Tutaj napiszemy więcej

Kalejdoskop

Oglądaj rysunki, wykonuj obliczenia, rozwiązuj zadania, formułuj swoje zdanie, próbuj je uzasadnić, ...

Tu znajdziesz ....

Obliczenia utemperowane

Utemperowane obliczenie dla n=76

Trzy zadania. Odpowiedz czy są one jakos powiązane?

  • Masz do dyspozycji bardzo wiele trójkątnych płytek, w dwu kolorach.

Czy potrafisz ułożyć chodnik łączący posesje o numerze n z numerem 1?

  • Ułamek piętrowy
  • Czy obliczenie 3x+1 jest skończone dla każdej liczby naturalnej?

Struktury algebraiczne

Struktura liczb naturalnych.
Algebra Jaśkowskiego.

Teorie

elementarna teoria liczb naturalnych z dodawaniem.
algorytmiczna teoria liczb naturalnych

Zadania

[math]\alpha[/math]

Archiwum kolejnych wersji pracy

[CollatzConjecturebecomesTheorem11Aug23 http://lem12.uksw.edu.pl/images/3/3b/CollatzConjecturebecomesTheorem11Aug23.pdf]

\On Collatz theorem II.pdf wersja z 5 czerwca 2022

]wersja z 20 wrzesnia 2021

algorytmy wokół Collatzowe

wersja z 27 wrzesnia 2021

wersja z 7 pażdziernika 2021

Źródło „https://lem12.uksw.edu.pl/index.php?title=Collatz&oldid=3096”