Collatz: Różnice pomiędzy wersjami
(→Formuła stopu) |
|||
| (Nie pokazano 109 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
Nareszcie!<br /> | Nareszcie!<br /> | ||
| + | |||
Praca nad problemem trwała 83 lata.<br /> | Praca nad problemem trwała 83 lata.<br /> | ||
| + | Udało się. Zmieniamy statut ''hipotezy Collatza'' na [http://lem12.uksw.edu.pl/images/3/37/CollatzConjecturebecomesTheorem20Nov23.pdf '''twierdzenie Collatza'''].<br /> | ||
| + | <big>Prośba</big><br /> | ||
| − | |||
| − | |||
| + | Wersja z 5 czerwca 2022 [https://dx.doi.org/10.2139/ssrn.4158238 '''twierdzenie Collatza'''] przedłozona do TCS Journal .<br /> | ||
| + | Skróconą i niezbyt formalną wersję dowodu znajdziesz w tym [http://lem12.uksw.edu.pl/images/9/9f/MainPointsProofCollatz.pdf miejscu].<br /> | ||
==Wprowadzenie== | ==Wprowadzenie== | ||
Rozpatrzmy zdanie<br/> | Rozpatrzmy zdanie<br/> | ||
| − | dla każdej liczby naturalnej <math>n</math>, poniższy program ma obliczenie sończone<br/> | + | dla każdej liczby naturalnej <math>n</math>, poniższy program <math>Cl </math> ma obliczenie sończone<br/> |
| − | { | + | <math>\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ |
| − | + | \quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ | |
| − | + | \mathbf{od} \end{array}\right\} </math> <br /> | |
| − | + | Zaczynamy od uwagi, że prawdziwośc powyższego zdania pociaga za sobą prawdzowość tezy Collatza, tak jak ona została sformułowana przed II wojną światową. <br /> | |
| − | + | Ale w r.1937 nie istniały komputery ani języki programowania<br /> | |
| − | + | .Z drugiej strony istniała i była już mocno rozwinięta teoria algorytmów. Teorię funkcji rekurencyjnych rozwijanow w Getyndze (David Hilbert i jego uczniowie), Budapeszcie (Rozsza Pterer, Laszlo Kalmar), ...<br /> | |
| + | W Londynie Alan Turing stworzył abstrakcyjną maszynę Turinga.<br /> | ||
| + | W Moskwie Kołmogorow i w Kazaniu Malcew badali pojęcie funkcji obliczalnej. <br /> | ||
| + | <br /> | ||
| + | W Warszawie Alfred Tarski wraz z uczniami Mojżeszem Presburgerem, Stanisławem Jaskowskim uzyskali ważne wyniki dotycące teorii dodawania liczb naturalnych. | ||
| + | |||
| + | ==Nasze spostrzeżenia z r. 2004== | ||
| + | * Algorytm Collatza <math>Cl</math> nie potrzebuje operacji mnożenia ani dzielenia. Wystarczy mnożenie przez 3 ( bo 3x=x+x+x) i dzielenia przez 2 ( prosty algorytm dodający co drugą jedynkę wystarczy), | ||
| + | * W strukturze algebraicznej <math>\mathfrak{M}</math>, która jest niestandardowym modelem elementarnej teorii dodawania liczb naturalnych (jest taka, zobacz poniżej) algorytm <math>Cl</math> ma dla wielu argumentów obliczenie nieskończone. | ||
| + | * A więc tezy Collatza nie można udowodnić na podstawie aksjomatów elementarnej teorii dodawania liczb naturalnych, | ||
| + | * Co więcej, w języku elementarnej teorii dodawania nie istnieje formuła stopu dl algorytmu Collatza!. Czego więc mamy dowieść? | ||
| − | + | ==Poprawne sformułowanie tezy Collatza== | |
| − | == | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
W standardowej strukturze liczb naturalnych z operacją dodawania | W standardowej strukturze liczb naturalnych z operacją dodawania | ||
| − | nasz program ma | + | nasz program <math>Cl</math> ma dla każdego argumentu ''n'' obliczenie skończone. |
| + | |||
==Formuła stopu== | ==Formuła stopu== | ||
| + | czyli | ||
| + | === Warunek konieczny i wystarczający na to by obliczenie było skończone=== | ||
Należy zatem stworzyć formułę <math>\theta</math> (wyrażenie logiczne) taką, że przyjmuje ona wrtośc prawda wtedy i tylko wtedy gdy obliczenie programu <math>Cl</math> jest skończone. Takich formuł jest wiele w języku urachunku programów, tj. logiki algorytmicznej.<br/> | Należy zatem stworzyć formułę <math>\theta</math> (wyrażenie logiczne) taką, że przyjmuje ona wrtośc prawda wtedy i tylko wtedy gdy obliczenie programu <math>Cl</math> jest skończone. Takich formuł jest wiele w języku urachunku programów, tj. logiki algorytmicznej.<br/> | ||
| − | ,<math> \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ | + | ,<math>\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\ |
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ | \quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ | ||
\mathbf{od} \end{array}\right\} (n=1) </math> | \mathbf{od} \end{array}\right\} (n=1) </math> | ||
<br /> | <br /> | ||
| − | Można też rozważać inne formuły. <br/> | + | Wartość formuły <math>\theta</math> zleży tylko od początkowej wartości zmiennej "n". Formuła ta jest spełniona przez wartość zmiennej "n" wtedy i tylko wtedy gdy obliczenie programu while ... jest skończone i końcowa wartość zmiennej "n" jest równa 1. <br /> |
| − | Druga część zadania jest znacznie trudniejsza: przeprowadzić dowód formuły stopu posiłkując się aksjomatami rachunku programów i aksjomatami algorytmicznej teorii liczb naturalnych.<br/> | + | Można też rozważać inne formuły, np, <br/> |
| + | ,<math>\qquad \xi:\,\bigcup \left\{\overbrace{\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\ | ||
| + | \quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\ | ||
| + | \mathbf{fi} \end{array} }^{K}\right\} (n=1) </math> <br/> | ||
| + | {co się czyta: ''istnieje taka iteracja ,<math>K^i</math> programu <math>K</math>, że po wykonaniu <math>K^i</math> spełniona jest równość'' <math>n=1</math> .} <br/> | ||
| + | Inaczej mówiąc, mamy do czynienia z kresem górnym wartości formuł <math>K^i(n=1)</math>, gdzie <math>i= 0,1,2 \dots</math>.<br /> | ||
| + | |||
| + | Druga część zadania jest znacznie trudniejsza: nalezy przeprowadzić dowód formuły stopu posiłkując się aksjomatami rachunku programów i aksjomatami algorytmicznej teorii liczb naturalnych.<br/> | ||
<br /> | <br /> | ||
| + | |||
| + | ==Elementarna teoria dodawania liczb naturalnych== | ||
| + | Poprzednia obserwacja stwierdzająca, że w tej teorii nie można przeprowadzić dowodu tezy Collatza pozostaje w mocy. Jednak, w dalszych rozważaniach pomocne będą własności niestandardowego modelu tej teorii a także parę twierdzeń tej teorii.<br /> | ||
| + | <br /> | ||
| + | Teoria ta jest wyznaczona przez podanie trzech składników: języka, logiki czyli operacji konsekencji oraz aksjomatów specyficznych dla tej teorii. <br /> | ||
| + | '''Język.''' Wyrażenia języka zbudowane są z następujących symboli: symbole zmiennych np. x,y,n, symbou + dwuargumentoweji operacji, symbolu = dwuargumentowej relacji, symboli 0,1 stałych i symboli funktorów logicznych oraz symboli pomocniczych np. nawiasy<br /> | ||
| + | . | ||
| + | Przykładami wyrażeń są ...<br /> | ||
| + | |||
| + | '''Logika.''' Operacja konsekwencji (wnioskowania) jest wyznaczona przez podanie aksjomatów logiki pierwszego rzędu i reguł wnioskowania. <br /> | ||
| + | '''Aksjomaty.''' | ||
| + | |||
| + | '''Modele arytmetyki Presburgera''' | ||
| + | Zgodnie z przewidywaniami ciąg standardowych wartości 0,1,2,3, ... jest modelem tej teorii. | ||
| + | |||
| + | Stanisław Jaśkowski in 1929 odkrył inny,niestandardowy model arytmetyki Presburgera. | ||
| + | |||
| + | [[Plik:MonStandardModel.png|center|thumb|600px|Nonstandard model of Presburger arithmetic]] | ||
| + | The universe of the model is a subset of the set of complex numbers <math>a+\imath b</math> | ||
| + | where <math>a \in \mathbb{Z} </math> i.e. a is an integer number and <math>b \in \mathbb{Q}^+ </math> is a positive rational number. Additionally, whenever <math>b=0 </math> we have <math>a>0</math>. | ||
| + | Addition is defined as usual addition of complex numbers. | ||
| + | |||
| + | Oba modele są obliczalne. Istnieją też modele nieobliczalne, dowolnie wysokiej mocy. | ||
| + | |||
| + | ==Algorytmiczna teoria liczb naturalnych== | ||
| + | * Język. Alfabet języka zawiera zbiór zmiennych, np. x,y. funktor + dwiargumentowego działania dodawania, dwie stałe 0 i 1, znak relacji = równości.<br /> | ||
| + | Termy (tj. wyrażenia nazwowe: jest to najmniejszy zbiór wyrażeeń zawierający zmienne, stałe i zamknięty ze wzgledu na lączenie dwu termów w ten sposób (t1 + t2).<br /> | ||
| + | Formuły. | ||
| + | * Logika. Rachunek programów. Rachunek programów zawiera w sobie logikę pierwszego rzędu. Język rachunku programów oprócz formuł pierwszego rzędu zaiera formuły algorytmiczne. Najprostsza taka formuła to napis składający się z programu i następującej po nim formuły (zwykle formuły pierwszego rzędu). | ||
| + | Do aksjomatów logiki pierszego rzędu należy dodać aksjomaty opisujące własności spójników programotwórczych, zob. [[Logika algorytmiczna]]. | ||
| + | Do reguł wnioskowania logiki pierwszego rzędu należy dodać reguły specyficzne dla rachunku programów. <br /> | ||
| + | |||
| + | * Aksjomaty teorii. <br /> | ||
| + | Tylko trzy formuły. <br /> | ||
| + | <math> | ||
| + | \begin{eqnarray} | ||
| + | \tag{ATN1} \forall_x\, x+1 \neq 0 &&\\ | ||
| + | \tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\ | ||
| + | \tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) && | ||
| + | \end{eqnarray} </math><br /> | ||
| + | |||
| + | Są to właściwie aksjomaty teorii następnika.<br/> | ||
| + | Formuła ATN1 stwierdza, że 0 nie jest następnikiem żadnej liczby naturalnej. <br/> | ||
| + | Formuła ATN2 stwierdza, że następnik jest funkcją róznowartosciową. <br/> | ||
| + | Formuła ATN3 stwierdza, że każda liczba naturalna jest ''osiągalna'' z zera przez dodanie skończonej liczby jedynek.<br/> | ||
| + | W tej teorii można napisać definicje działań dodawania, mnożenia i każdej funkcji obliczalnej. | ||
| + | |||
| + | ==Analiza formuły stopu== | ||
| + | xxx | ||
| + | |||
| + | ==Trójki == | ||
| + | Spostrzeżenie (wynikłe z przygladania się formule stopu).<br /> | ||
| + | |||
| + | <math>\forall_{n \neq 0} \exists_{x,y,z}\ n \cdot 3^x+y=2^z </math> | ||
| + | |||
| + | ==Drzewo Collatza== | ||
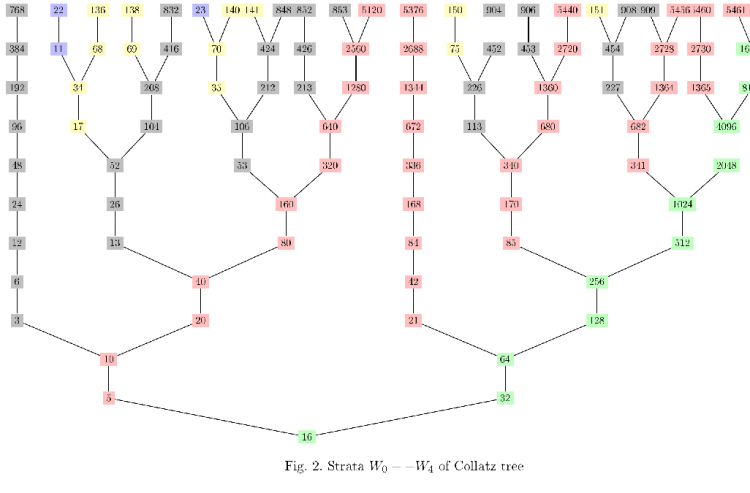
| + | [[Plik:StratDrzewoCollatza.png|thumb|center |750px| Rys. 1 Fragmenty warstw <math>W_0, \dots W_4 </math> drzewa Collatza ]] | ||
| + | |||
| + | ==Własności obliczeń na trójkach== | ||
| + | Tutaj napiszemy więcej<br /> | ||
| + | ==Kalejdoskop== | ||
| + | |||
| + | Oglądaj rysunki, wykonuj obliczenia, rozwiązuj zadania, formułuj swoje zdanie, próbuj je uzasadnić, ...<br /> | ||
| + | |||
| + | Tu znajdziesz ....<br /> | ||
| + | ===Obliczenia utemperowane=== | ||
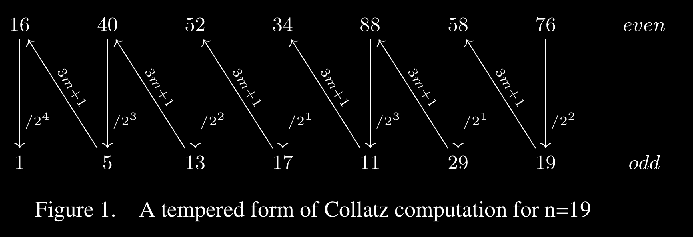
| + | [[Plik:ObliczN19.pdf.png|thumb|center|750px|Utemperowane obliczenie dla n=76]] | ||
| + | Trzy zadania. Odpowiedz czy są one jakos powiązane?<br /> | ||
| + | * Masz do dyspozycji bardzo wiele trójkątnych płytek, w dwu kolorach. | ||
| + | Czy potrafisz ułożyć chodnik łączący posesje o numerze n z numerem 1? | ||
| + | *[[Ułamek piętrowy]] | ||
| + | * Czy obliczenie 3x+1 jest skończone dla każdej liczby naturalnej? | ||
| + | |||
| + | ===Struktury algebraiczne=== | ||
| + | Struktura liczb naturalnych. <br /> | ||
| + | Algebra Jaśkowskiego.<br /> | ||
| + | ===Teorie=== | ||
| + | elementarna teoria liczb naturalnych z dodawaniem.<br /> | ||
| + | algorytmiczna teoria liczb naturalnych<br /> | ||
| + | ===Zadania=== | ||
| + | |||
| + | |||
| + | <math>\alpha</math><br /> | ||
| + | |||
| + | == Archiwum kolejnych wersji pracy == | ||
| + | [CollatzConjecturebecomesTheorem11Aug23 http://lem12.uksw.edu.pl/images/3/3b/CollatzConjecturebecomesTheorem11Aug23.pdf] | ||
| + | |||
| + | [https://dx.doi.org/10.2139/ssrn.4158238 \On Collatz theorem II.pdf wersja z 5 czerwca 2022 ] | ||
| + | |||
| + | ][http://lem12.uksw.edu.pl/images/a/ab/On-Collatz-thm17-09-21.pdf wersja z 20 wrzesnia 2021] | ||
| + | |||
| + | [http://lem12.uksw.edu.pl/images/7/7d/Algorytmy-bliskie-Collatzowi.pdf algorytmy wokół Collatzowe] | ||
| + | |||
| + | [http://lem12.uksw.edu.pl/images/c/c0/On-Collatz-thm-27-09-21.pdf wersja z 27 wrzesnia 2021] | ||
| + | |||
| + | [http://lem12.uksw.edu.pl/images/8/8f/On-Collatz-thm-7-10-21.pdf wersja z 7 pażdziernika 2021] | ||
Aktualna wersja na dzień 05:56, 25 cze 2025
Nareszcie!
Praca nad problemem trwała 83 lata.
Udało się. Zmieniamy statut hipotezy Collatza na twierdzenie Collatza.
Prośba
Wersja z 5 czerwca 2022 twierdzenie Collatza przedłozona do TCS Journal .
Skróconą i niezbyt formalną wersję dowodu znajdziesz w tym miejscu.
Spis treści
- 1 Wprowadzenie
- 2 Nasze spostrzeżenia z r. 2004
- 3 Poprawne sformułowanie tezy Collatza
- 4 Formuła stopu
- 5 Elementarna teoria dodawania liczb naturalnych
- 6 Algorytmiczna teoria liczb naturalnych
- 7 Analiza formuły stopu
- 8 Trójki
- 9 Drzewo Collatza
- 10 Własności obliczeń na trójkach
- 11 Kalejdoskop
- 12 Archiwum kolejnych wersji pracy
Wprowadzenie
Rozpatrzmy zdanie
dla każdej liczby naturalnej [math]n[/math], poniższy program [math]Cl [/math] ma obliczenie sończone
[math]\color{blue}\qquad Cl:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
\mathbf{od} \end{array}\right\} [/math]
Zaczynamy od uwagi, że prawdziwośc powyższego zdania pociaga za sobą prawdzowość tezy Collatza, tak jak ona została sformułowana przed II wojną światową.
Ale w r.1937 nie istniały komputery ani języki programowania
.Z drugiej strony istniała i była już mocno rozwinięta teoria algorytmów. Teorię funkcji rekurencyjnych rozwijanow w Getyndze (David Hilbert i jego uczniowie), Budapeszcie (Rozsza Pterer, Laszlo Kalmar), ...
W Londynie Alan Turing stworzył abstrakcyjną maszynę Turinga.
W Moskwie Kołmogorow i w Kazaniu Malcew badali pojęcie funkcji obliczalnej.
W Warszawie Alfred Tarski wraz z uczniami Mojżeszem Presburgerem, Stanisławem Jaskowskim uzyskali ważne wyniki dotycące teorii dodawania liczb naturalnych.
Nasze spostrzeżenia z r. 2004
- Algorytm Collatza [math]Cl[/math] nie potrzebuje operacji mnożenia ani dzielenia. Wystarczy mnożenie przez 3 ( bo 3x=x+x+x) i dzielenia przez 2 ( prosty algorytm dodający co drugą jedynkę wystarczy),
- W strukturze algebraicznej [math]\mathfrak{M}[/math], która jest niestandardowym modelem elementarnej teorii dodawania liczb naturalnych (jest taka, zobacz poniżej) algorytm [math]Cl[/math] ma dla wielu argumentów obliczenie nieskończone.
- A więc tezy Collatza nie można udowodnić na podstawie aksjomatów elementarnej teorii dodawania liczb naturalnych,
- Co więcej, w języku elementarnej teorii dodawania nie istnieje formuła stopu dl algorytmu Collatza!. Czego więc mamy dowieść?
Poprawne sformułowanie tezy Collatza
W standardowej strukturze liczb naturalnych z operacją dodawania nasz program [math]Cl[/math] ma dla każdego argumentu n obliczenie skończone.
Formuła stopu
czyli
Warunek konieczny i wystarczający na to by obliczenie było skończone
Należy zatem stworzyć formułę [math]\theta[/math] (wyrażenie logiczne) taką, że przyjmuje ona wrtośc prawda wtedy i tylko wtedy gdy obliczenie programu [math]Cl[/math] jest skończone. Takich formuł jest wiele w języku urachunku programów, tj. logiki algorytmicznej.
,[math]\qquad \theta:\,\left\{\begin{array}{l} \mathbf{while}\ n \neq 0 \ \mathbf{do} \\
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
\mathbf{od} \end{array}\right\} (n=1) [/math]
Wartość formuły [math]\theta[/math] zleży tylko od początkowej wartości zmiennej "n". Formuła ta jest spełniona przez wartość zmiennej "n" wtedy i tylko wtedy gdy obliczenie programu while ... jest skończone i końcowa wartość zmiennej "n" jest równa 1.
Można też rozważać inne formuły, np,
,[math]\qquad \xi:\,\bigcup \left\{\overbrace{\begin{array}{l} \mathbf{if}\ n \neq 0 \ \mathbf{then} \\
\quad \mathbf{if}\ nieparzyste(n) \ \mathbf{then}\ n:=3n+1 \ \mathbf{else}\ n:=n/2\ \mathbf{fi} \\
\mathbf{fi} \end{array} }^{K}\right\} (n=1) [/math]
{co się czyta: istnieje taka iteracja ,[math]K^i[/math] programu [math]K[/math], że po wykonaniu [math]K^i[/math] spełniona jest równość [math]n=1[/math] .}
Inaczej mówiąc, mamy do czynienia z kresem górnym wartości formuł [math]K^i(n=1)[/math], gdzie [math]i= 0,1,2 \dots[/math].
Druga część zadania jest znacznie trudniejsza: nalezy przeprowadzić dowód formuły stopu posiłkując się aksjomatami rachunku programów i aksjomatami algorytmicznej teorii liczb naturalnych.
Elementarna teoria dodawania liczb naturalnych
Poprzednia obserwacja stwierdzająca, że w tej teorii nie można przeprowadzić dowodu tezy Collatza pozostaje w mocy. Jednak, w dalszych rozważaniach pomocne będą własności niestandardowego modelu tej teorii a także parę twierdzeń tej teorii.
Teoria ta jest wyznaczona przez podanie trzech składników: języka, logiki czyli operacji konsekencji oraz aksjomatów specyficznych dla tej teorii.
Język. Wyrażenia języka zbudowane są z następujących symboli: symbole zmiennych np. x,y,n, symbou + dwuargumentoweji operacji, symbolu = dwuargumentowej relacji, symboli 0,1 stałych i symboli funktorów logicznych oraz symboli pomocniczych np. nawiasy
.
Przykładami wyrażeń są ...
Logika. Operacja konsekwencji (wnioskowania) jest wyznaczona przez podanie aksjomatów logiki pierwszego rzędu i reguł wnioskowania.
Aksjomaty.
Modele arytmetyki Presburgera Zgodnie z przewidywaniami ciąg standardowych wartości 0,1,2,3, ... jest modelem tej teorii.
Stanisław Jaśkowski in 1929 odkrył inny,niestandardowy model arytmetyki Presburgera.
The universe of the model is a subset of the set of complex numbers [math]a+\imath b[/math] where [math]a \in \mathbb{Z} [/math] i.e. a is an integer number and [math]b \in \mathbb{Q}^+ [/math] is a positive rational number. Additionally, whenever [math]b=0 [/math] we have [math]a\gt0[/math]. Addition is defined as usual addition of complex numbers.
Oba modele są obliczalne. Istnieją też modele nieobliczalne, dowolnie wysokiej mocy.
Algorytmiczna teoria liczb naturalnych
- Język. Alfabet języka zawiera zbiór zmiennych, np. x,y. funktor + dwiargumentowego działania dodawania, dwie stałe 0 i 1, znak relacji = równości.
Termy (tj. wyrażenia nazwowe: jest to najmniejszy zbiór wyrażeeń zawierający zmienne, stałe i zamknięty ze wzgledu na lączenie dwu termów w ten sposób (t1 + t2).
Formuły.
- Logika. Rachunek programów. Rachunek programów zawiera w sobie logikę pierwszego rzędu. Język rachunku programów oprócz formuł pierwszego rzędu zaiera formuły algorytmiczne. Najprostsza taka formuła to napis składający się z programu i następującej po nim formuły (zwykle formuły pierwszego rzędu).
Do aksjomatów logiki pierszego rzędu należy dodać aksjomaty opisujące własności spójników programotwórczych, zob. Logika algorytmiczna.
Do reguł wnioskowania logiki pierwszego rzędu należy dodać reguły specyficzne dla rachunku programów.
- Aksjomaty teorii.
Tylko trzy formuły.
[math]
\begin{eqnarray}
\tag{ATN1} \forall_x\, x+1 \neq 0 &&\\
\tag{ATN2} \forall_{x,y}\,x+1=y+1 \implies x=y &&\\
\tag{ATN3}\forall_x\, \{y :=0; \mathbf{while}\ y\neq x\ \mathbf{do}\ y:=y+1\ \mathbf{od} \}\,(y=x) &&
\end{eqnarray} [/math]
Są to właściwie aksjomaty teorii następnika.
Formuła ATN1 stwierdza, że 0 nie jest następnikiem żadnej liczby naturalnej.
Formuła ATN2 stwierdza, że następnik jest funkcją róznowartosciową.
Formuła ATN3 stwierdza, że każda liczba naturalna jest osiągalna z zera przez dodanie skończonej liczby jedynek.
W tej teorii można napisać definicje działań dodawania, mnożenia i każdej funkcji obliczalnej.
Analiza formuły stopu
xxx
Trójki
Spostrzeżenie (wynikłe z przygladania się formule stopu).
[math]\forall_{n \neq 0} \exists_{x,y,z}\ n \cdot 3^x+y=2^z [/math]
Drzewo Collatza
Własności obliczeń na trójkach
Tutaj napiszemy więcej
Kalejdoskop
Oglądaj rysunki, wykonuj obliczenia, rozwiązuj zadania, formułuj swoje zdanie, próbuj je uzasadnić, ...
Tu znajdziesz ....
Obliczenia utemperowane
Trzy zadania. Odpowiedz czy są one jakos powiązane?
- Masz do dyspozycji bardzo wiele trójkątnych płytek, w dwu kolorach.
Czy potrafisz ułożyć chodnik łączący posesje o numerze n z numerem 1?
- Ułamek piętrowy
- Czy obliczenie 3x+1 jest skończone dla każdej liczby naturalnej?
Struktury algebraiczne
Struktura liczb naturalnych.
Algebra Jaśkowskiego.
Teorie
elementarna teoria liczb naturalnych z dodawaniem.
algorytmiczna teoria liczb naturalnych
Zadania
[math]\alpha[/math]
Archiwum kolejnych wersji pracy
[CollatzConjecturebecomesTheorem11Aug23 http://lem12.uksw.edu.pl/images/3/3b/CollatzConjecturebecomesTheorem11Aug23.pdf]