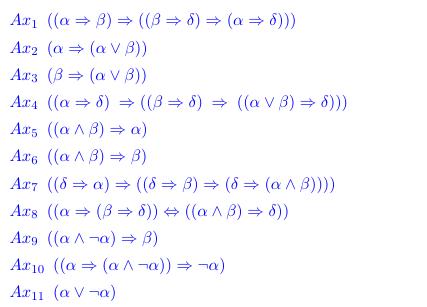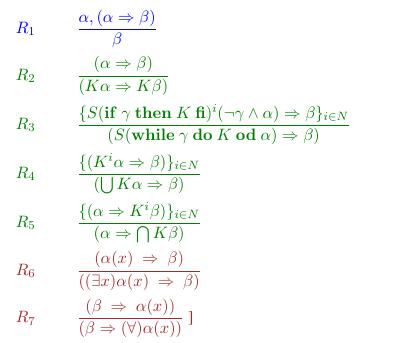Algorithmic Logic
This page is under construction
Felix qui potuit rerum cognoscere causas
Algorithmic logic is a calculus in which one can express the semantical properties of programs and it allows to construct proofs of the formulas. In this way one can prove property like correctness by proving the corresponding formula that express the property.
Spis treści
Introduction
Algorithmic logic is a calculus of logic. It is an attractive workplace for software engineers as well as for mathematially oriented people. It is quite reasonable to give it another name calculus of programs.
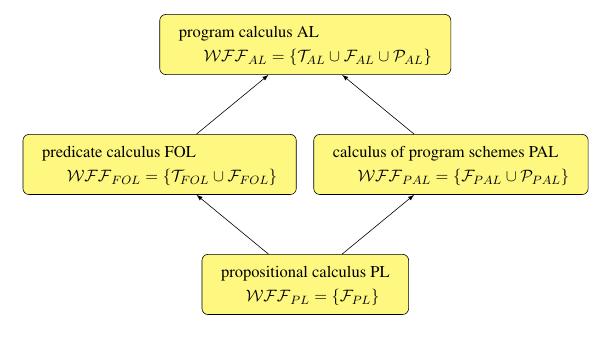
Figure 1 shows relations among four logical calculi. An arrow [math]\mathcal{L}\rightarrow\mathcal{L}'[/math] between two logical calculi [math]\mathcal{L}[/math] and [math]\mathcal{L}'[/math] has following meaning: Every tautology [math]\alpha[/math] of calculus [math]\mathcal{L}[/math] becmes a tatutology of calculus [math]\mathcal{L}[/math]' when atoms of formula [math]\alpha[/math] are replaced by formulas of calculus [math]\mathcal{L}[/math]. More insight can be gained by comparison of sets of well formed formulas [math]\mathcal{WFF} [/math].
The languages of four calculi differ. Each language is a pair <alphabet, WFF the set of well formed expressions>. Note, in each case the structure of the set of well formed expression [math]\mathcal{WFF} [/math] (ang. well formed formulas) is different.
Legend: [math]\mathcal{L}[/math] - language, [math]\mathcal{A}[/math] - alphabet, [math]\mathcal{T}[/math] - set of terms (arithmetical, object, string, ... expressions), [math]\mathcal{F}[/math] - set of formulas, [math]\mathcal{P}[/math] - set of programs.
Set of formulas of algorithmic logic contains all formulas of first-order logic. Moreover it contains formulas which consist of program preceding a formula. If [math]\alpha[/math] is a formula and [math]K[/math] is a program, then the expression of the form [math]K\alpha[/math] is a formula of the language of algorithmic logic. In short, an algorithmic formula.
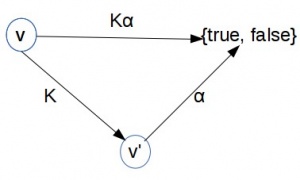
Such a formula [math]K\alpha[/math] is evaluated to false or true according to the diagram Fig.5.
Figure 5 should be self explanatory. It remains to decide what to do when a computation of program K does not bring a result . It may happen that computation of program K is infinite or another error occurred. In such case it is impossible to assert that for data v the computation of program K ends successfully and the results satisfy the condition [math]\alpha[/math]'. Hence in this case the value of formula [math]K\alpha[/math] is false..
O logice algorytmicznej możemy też powiedzieć, że jest rachunkiem programów. Język logiki algorytmicznej zawiera programy i formuły algorytmiczne. Ważne jest to, że każda semantyczna własność programów np. poprawność, równowazność, kończenie obliczeń lub przeciwnie zapętlanie, ... może być wyrażona przez odpowiednią formułę. Pozwala to zamienić zadanie wykazania, że pewien program [math]P[/math] posiada pewną własnośc semantyczną [math]S[/math] na zadanie udowodnić formułę [math]\beta[/math] należąca do języka logiki algorytmicznej.
Przykład
Własność: Dla każdych danych [math]v[/math], jeśli program [math]K[/math] rozpoczyna obliczenia z danymi spełniającymi warunek [math]\alpha[/math] to jego obliczenie zakończy się (nie będzie zapętlenia, ani przerwania obliczeń) i jego wyniki spełniają warunek [math]\beta[/math], jest wyrażana formułą [math]\alpha \rightarrow K\beta[/math]. Nie musimy więc podejmować trudu testowania czy dla kazdych danych obliczenie programu K będzie skończone i ...
Formuły tworzą algebrę z działaniami: konkatenacji, alternatywy, negacji i implikacji oraz z działaniami nieskończonymi tj. kwantyfikatorami, ponadto programy są modalnościami. Programy też tworzą algebrę: działaniami tej algebry są iteracja, rozgałęzienie i złożenie programów. Mamy więc do czynienia ze splotem dwu algebr. Możemy go nazwać rachunkiem programów. Zadaniem logiki algorytmicznej jest poszukiwanie praw rachunku programów.
Celem jest zebranie praw i reguł wnioskowania, które umożliwią analizę algorytmów i wydawanie opinii o ich własnościach semantycznych, bez wykonywania obliczeń, na podstawie samego tekstu algorytmu i aksjomatów struktury danych w jakiej dany program ma byc interpretowany.
Structure of AL
An algorithmic logic is a pair [math]\mathcal{AL} = \langle \mathcal{L}, \mathcal{C} \rangle [/math], where [math]\mathcal{L} [/math] is a formalized language of algorithmic logic and [math]\mathcal{C} [/math] is i a logical consequence operation defined by the notions of logical axioms, inference rules and the notion of (formal) proof. An algorithmic language [math]\mathcal{L} [/math] is a pair consisting of the alphabet of [math]\mathcal{L} [/math] and the set of well-formed expressions, [math]\mathcal{L} = \langle A, WFF \rangle [/math], where [math] A [/math] is the alphabet, i.e. the set of admissible symbols and [math] WFF [/math] is the set of well formed expressions of the language.
Structure
- Define syntax - of expressions(terms), formulas and programs.
- Define semantics - partially using the Tarski's scheme: each term defines a function and each formula defines ...
- partially through the notion of computation ...
- Make a catalogue of semantical properties of programs: halting property, correctness, partial correctness, ...
- Define algorithmic formulas -- show that semantical properties of programs are expressible in the language of algorithmic formulas,
- Find the axioms and inference rules of algorithmic logic
- Show the completeness property of AL,
- Show applications
Algorithmic theories
Here we shall collect axiomatization of various algorithmic theories. Each set [math]S[/math] of this collection may be conceived as specification of a class [math]C[/math] that implements the set [math]S[/math].
Algorithmic theory of natural numbers
The theory of one constant 0, one one-argument functor [math]s[/math] and predicate of equality =.
Axioms
[math]\begin{align*}
& \forall_n s(n) \neq 0 \\
& \forall_n \forall_m s(n)=s(m) \implies n=m \\
& \forall_n \{m:=0; \mathbf{while}\ n\neq m\ \mathbf{do}\ m:=s(m)\ \mathbf{od} \}(n=m)
\end{align*} [/math]
Algorithmic theory of integers
Liczby całkowite tworzą zbiór oznaczany integer (lub [math]Z[/math]), razem z niepustym podzbiorem [math]N[/math] (liczb całkowitych nieujemnych) i z dwoma operacjami dwuargumentowymi dodawania i mnożenia, oznaczanymi przez [math]+[/math] i [math]\cdot[/math], które spełniają następujące aksjomaty:
- (Przemienność) Dla każdej pary liczb całkowitych [math]a, b[/math] zachodzą równości
</math>a+b=b+a</math> \ \ \ oraz\ \ \ [math]a\cdot b = b \cdot a[/math],
- (Łączność) Dla każdej trójki liczb całkowitych [math]a,b, c[/math] zachodzą
[math](a+(b+c))=((a+b)+c) [/math] \ \ \ oraz\ \ \ [math](a\cdot(b\cdot c))=((a\cdot b)\cdot c)[/math],
- (Rozdzielność) Dla każdej trójki liczb całkowitych zachodzi
[math](a+b)\cdot c =a\cdot c + b\cdot c[/math]
- (Jedności) Istnieją liczby całkowite 0 i 1 takie, że dla każdego [math]a[/math] zachodzi
[math]a+0=a[/math] \ \ \ oraz\ \ \ [math]a\cdot 1= a[/math],
- (Domknięcie w [math]N[/math]) Jeśli [math]a[/math] i [math]b[/math] są liczbami całkowitymi nieujemnymi to liczby [math]a+b[/math] oraz [math]a\cdot b[/math] też są liczbami całkowitymi, nieujemnymi,
- (Addytywna odwrotność) Dla każdej liczby całkowitej [math]a[/math], istnieje taka liczba całkowita [math]-a[/math], że za
[math] a+-a =0 [/math]
- (Trichotomia) Dla każdej liczby całkowitej [math]a[/math] zachodzi dokładnie jedna z trzech relacji: albo a) liczba [math]a[/math] jest nieujemna, albo b) liczba [math]a[/math] jest zerem [math]a=0[/math] albo c) liczba [math]-a[/math] jest nieujemna,
- (Liczby całkowite nieujemne) Zbiór liczb całkowitych nieujemnych spełnia aksjomaty liczb naturalnych, to jest ten sam zbiór.
I to na tyle
Algorithmic theory of rational numbers
Axioms of ordered field and algorithmic formula saying for all n and m the Euclid's algorithm terminates.
History
The first papers on properties of programs appeared in the 50-ies of XX century. To mention a few: Yanov, Sh. Igarashi. Later the papers of Helmut Thiele and of Erwin Engeler are important ones.
In 1969 the program of research of algorithmic logic was formulated in the Ph.D. thesis of A. Salwicki.
Floyd-Hoare logic
Paper of R.W. Floyd brought some light on proving programs correct. Later C.A.R. Hoare proposed another formalization based on the ideas of Floyd. S. Cook addressed the problem of completeness of Floyd-Hoare calculus and formulated the so called relative completeness theorem.
In the light of the paper [Goraj, Mirkowska, Paluszkiewicz ↓] this theorem is unnecessary. Theorem 5 of this paper states that notions of feasible and of acceptable description of program coincide. In other words if a verification condition of a program is valid in all models of a theory then it is provable from the axioms of the theory. For the details see [AL4software ↓] sections on Floyd's descriptions of programs and Hoare's logic of partial correctness.
Bibliography
Books
- [AlgoLog] Grażyna Mirkowska, Andrzej Salwicki: Algorithmic Logic. Warszawa: PWN, 1987, s. 345.
- [LogProg1] Grażyna Mirkowska, Andrzej Salwicki: Logika Algorytmiczna dla Programistów. Warszawa: WNT, 1992, s. 294. cz.1
- [LogProg2] Grażyna Mirkowska, Andrzej Salwicki: Logika Algorytmiczna dla Programistów. Warszawa: WNT, 1992, s. 294. cz.2
- [AL4software] Grażyna Mirkowska, Andrzej Salwicki: Algorithmic Logic for Software Construction and Verification. Dąbrowa Leśna: Dąbrowa Research, 2014, s. 154.
- [CentrumBanachAL] Lech Banachowski, Antoni Kreczmar, Grażyna Mirkowska, Helena Rasiowa, Andrzej Salwicki: An introduction to Algorithmic Logic - Metamathematical Investigations of Theory of Programs. T. 2: Banach Center Publications. Warszawa: PWN, 1977, s. 7-99, seria: Banach Center Publications. ISBN 123.
- [HRAL] Helena Rasiowa: Algorithmic Logic - Notes from Seminar in Simon Fraser University. T. 281. Warsaw: 1975, seria: Reports of Institute of Computer Science PAS.
- [AB] Andrzej Biela: Algorithmic structural completeness and a retrieval system for proving theorems in algorithmic theories. T. 1901. Katowice: Wydawnictwo Uniwersytetu Śląskiego, 2000, s. 122.
A choice of publications
- [GMP] Anna Góraj, Grazyna Mirkowska, Anna Paluszkiewicz. On the notion of description of program. „Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys.”, s. 499 - 505, 1970.
- [GM1971] Grażyna Mirkowska. On Formalized Systems of Algorithmic Logic. „Bull. Polish Academy Sciences, Ser. Math. Phys.”, s. 421-428, 1971.
- [GM1] Grazyna Mirkowska. Algorithmic logic and its applications in the theory of programs I. „Fundamenta Informaticae”, s. 1-17, 1977.
- [GM2] Grazyna Mirkowska. Algorithmic logic and its applications in the theory of programs II. „Fundamenta Informaticae”, s. 147-165, 1977.
- [AS1] Andrzej Salwicki. Formalized Algorithmic Languages. „Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys.”, s. 227-232, 1970.
- [AS3] Andrzej Salwicki. On the predicate calculi with iteration quantifiers. „Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys.”, s. 279-285, 1970.
- [LB1] Lech Banachowski. Investigations of Properties of Programs by means of Extended Algorithmic Logic I. „Fundamenta Informaticae”, s. 93-119, 1977.
- [LB2] Lech Banachowski. Investigations of Properties of Programs by means of Extended Algorithmic Logic II. „Fundamenta Informaticae”, s. 167-193, 1977.
- [LB3] Lech Banachowski. An Axiomatic Approach to the Theory of Data Structures. „Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys.”, s. 315-323, 1975.
- [AK1] Antoni Kreczmar. Programmability in Fields. „Fundamenta Informaticae”, s. 195-230, 1977.
- [AK2] Antoni Kreczmar. Effectivity problems of Algorithmic Logic. „Fundamenta Informaticae”, s. 19-32, 1977.
- [MSS2009] Grażyna Mirkowska, Andrzej Salwicki, Oskar Świda. Verifying a Class: combining Testing and Proving. „Fundamenta Informaticae”, s. 305-324, 2009.
- [AS2017] Andrzej Salwicki. A new proof of Euclid's algorithm. .
Other papers
- [Yanov 1959] Yuri I. Yanov. The Logical schemes in Algorithms. „Problems of Cybernetics”, s. 82-140, 1959.
- [Engeler 1967 ] Erwin Engeler. Algorithmic properties of Structures. „Math. System Theory”, s. 183-195, 1967.